There are mainly two methods that can be used to represent a set. The Listing method is also called the roster method. This method shows the list of all the elements of a set inside brackets. The elements are written only once and are separated by commas. For example, a set consisting of all even positive integers less than 11 is represented in roster form as and in set-builder form, it is represented as . In set builder notation, we define a set by describing the properties of its elements instead of listing them.
This method is especially useful when describing infinite sets. Roster notation of a set is a simple mathematical representation of the set in mathematical form. In the roster form, the elements of a set are listed in a row inside the curly brackets. Every two elements are separated by a comma symbol in a roster notation if the set contains more than one element. The roster form is also called the enumeration notation as the enumeration is done one after one. The contents of a set can be described by listing the elements of the set, separated by commas, inside a set of curly brackets.
This way of describing a set is called roster form . This way of describing a set is called roster form. Roster notation is one of the most simple techniques to represent the elements of a set.
A method of listing the elements of a set in a row with comma separation within curly brackets is called the roster notation. In this, a rule, or the formula or the statement is written within the pair of brackets so that the set is well defined. In the set builder form, all the elements of the set, must possess a single property to become the member of that set. /Q/What_is_roster_notation_method What is roster notation method? - Answers This is a method describing a set by listing each element of the set inside the symbol .
In listing the elements of the set, each distinct element is listed once and the order of the elements does not matter. The roster notation is a simple mathematical representation of a set in mathematical form. In this method, the elements are enumerated in a row inside the curly brackets. If the set contains more than one element, then every two elements are separated by a comma symbol. It is not actually possible to express all of them in roster form.
Similarly, we don't know the last element in these types of sets. If sets follow a pattern or have a particular sequence, we just write the first three or four elements with a continuous symbol within the curly braces. The above set has only 3 elements, so it would not be difficult to write it in roster form as shown above.
However, if your set has hundreds or thousands of elements, it would be hard to list them out, but easy to refer to them using set builder notation. The objects that are used to form a set are called its elements or its members. In general, the elements of a set are written inside the curly braces and separated by commas. The name of the set is always written in capital letters.
Set Builder Notations is the method to describe the set while describing the properties and not just listing its elements. When there is set formation in a set builder notation then it is called comprehension, set an intention, and set abstraction. The set can be defined by listing all its elements, separated by commas and enclosed within braces. The roster method is defined as a way to show the elements of a set by listing the elements inside of brackets.
An example of the roster method is to write the set of numbers from 1 to 10 as . An example of the roster method is to write the seasons as . A method of listing the elements in a row with comma separation within curly brackets is called the roster notation. In sets theory, you will learn about sets and it's properties. It was developed to describe the collection of objects. You have already learned about the classification of sets here.
The set theory defines the different types of sets, symbols and operations performed. The method of defining a set by describing its properties rather than listing its elements is known as set builder notation. To write T in roster form, we first figure out all of its elements. We see that T consists of all elements, x, such that x is prime and 3 ≤ x ≤ 10. Prime numbers are positive integers that are only divisible by 1 and themselves, so T is all the integers between 3 and 10 that are only divisible by 1 and themselves. Now we just list them, separated by commas, within braces.
A set with no members is called an empty, or null, set, and is denoted ∅. The elements in a set can be represented in a number of ways, some of which are more useful for mathematical treatment and others for general understanding. These different methods of describing a set are called set notations. Though roster form of a set is probably the most basic and simple way to represent a set, it's not always the best way. In answering these questions, we'll see the limitations of roster form. First of all, the set of all real numbers is an infinite set.
That is, it has an infinite number of elements in it. Therefore, it's impossible to list all of the real numbers. However, we can accommodate this by using three periods. Basically, to represent a set in roster form, we simply list the elements of the set, separated by commas, within braces. Now that we're familiar with what the roster form of a set is, let's dig a bit deeper.
So far we specified the elements of sets by verbally. The roster form introduced here offers a concise way of writing down sets by listing all elements of the set. Furthermore we use ellipsis to describe the elements in a set, when we believe that the reader understands how a pattern in a list of elements continues. Each object in the set is called an element of the set. If an element x is a member of the set S, we write . If an element x is not a member of the set S, we write .
The empty set is the set that contains no elements. For sets A and B, A is called a subset of B, denoted , if every element of A is also an element of B. In this article, we learned about sets, properties of sets, and elements of a set. Then we learned about the three methods to represent a set- Description Method, Roster or Tabular Method, and Rule or Set-Builder Method. In addition to this, we learned to convert the roster form to set-builder form and vice versa.
Furthermore, we learnt the cardinality of a set. The definitions of these numbers may be somewhat elaborate. However, the important thing to realize is that each type of number listed above is aninfinite set, and that set-builder notation is often used to describe such sets. Let's look at some examples of set-builder notation. This is best used to represent the sets mainly with an infinite number of elements. It is used commonly with integers, real numbers, and natural numbers.
This also is used to represent the sets with intervals and equations. Students have to be very clear and learn precisely so that they can solve any problem related to the topic. Students can refer to Vedantu and learn the chapter clearly with a detailed explanation of every topic. Set builder notation contains one or two variables and also defines which elements belong to the set and the elements which do not belong to the set. The rule and the variables are separated by slash and colon.
This is often used for describing infinite sets. In maths, the letter R denotes the set of all real numbers. Real numbers are the numbers that include, natural numbers, whole numbers, integers, and decimal numbers. In other words, real numbers are defined as the points on an infinitely extended line.
The set of integers is represented by the letter Z. Integers are sometimes split into 3 subsets, Z+, Z- and 0. Z+ is the set of all positive integers , while Z- is the set of all negative integers (, -3, -2, -1). Zero is not included in either of these sets .
Rule Method This method involves specifying a rule or condition which can be used to decide whether an object can belong to the set. A set, informally, is a collection of things. The "things" in the set are called the "elements", and are listed inside curly braces. Observing the relationships between the set elements and writing the condition as a statement to change from roster form to set builder form.
In this method, a well-defined description of the elements of a set is made. At times, the definition of elements is enclosed within the curly brackets. The elements of a set are written inside a pair of curly braces and separated by commas. In this case, the description of the common property of the elements of a set is written inside the braces.
This is the simple form of a set-builder form or rule method. We see lists of objects all the time in the world around us. This lesson will explain how to represent a set in roster form, or as a list of elements. We will also look at some pros and cons to roster form of a set. Set notation is used to help define the elements of a set. The symbols shown in this lesson are very appropriate in the realm of mathematics and in mathematical logic.
When done properly, a set described in words or in symbols will clearly show all the elements of that set. One of the limitations of roster notation is that we cannot represent a large number of data in roster form. For example, if we want to represent the first 100 or 200 natural numbers in a set B then it is hard for us to represent this much data in a single row.
This limitation can be overcome by representing data with the help of a dotted line. Take a set of the first 100 positive odd numbers and represent using roster notation. Listing all the elements of a set, separated by commas and enclosed within curly brackets $$\left\ \right\$$. It's a method describing a set by listing each element of the set inside the symbol . In listing the elements of the set, each distinct elements is listed once and the order of the elements does not matter. The expression "$\$" is commonly pronounced as "The set of integers such that $1\lt n$ and $n\lt6$." This means exactly the set $\$.
Students whose native language does not have definite articles sometimes assume that a set such as $\$ fits the description. Of any set \(A\) is the set of all subsets of \(A,\) including the empty set and \(A\) itself. It is denoted by \(\mathcal\left( A \right)\) or \(.\) If the set \(A\) contains \(n\) elements, then the power set \(\mathcal\left( A \right)\) has \(\) elements.
The sets are of different types, such as empty set, finite and infinite set, equal set, equivalent set, proper set, disjoint set, subsets, singleton set. They are empty set, finite and infinite sets, proper set, equal sets, etc. Let us go through the classification of sets here. In statement form, the well-defined descriptions of a member of a set are written and enclosed in the curly brackets. Sets are represented as a collection of well-defined objects or elements and it does not change from person to person. The number of elements in the finite set is known as the cardinal number of a set.
Sets are arguably the most fundamental objects in modern mathematics. Familiarity with set notation is a prerequisite to reading post-secondary mathematics. What follows is a brief summary of key definitions and concepts related to sets required in this course. En.wikipedia.org/wiki/Set_ Set mathematics - Wikipedia In mathematics, a set is a collection of distinct elements or members. Two sets are equal if and only if they have precisely the same elements.
This is known as the axiom of extensionality. Here we are going to see examples on roster form and set builder form. Listing the elements of a set inside a pair of braces is called the roster form. In subsequent efforts to resolve these paradoxes since the time of the original formulation of naïve set theory, the properties of sets have been defined by axioms.
Axiomatic set theory takes the concept of a set as a primitive notion. The set can be defined by describing the elements using mathematical statements. This method is also called the tabulation method. When using this method, we list the elements of the set in a row between curly braces.
We can write the domain of f in set builder notation as, . To write this in roster form, we would first identify all the elements in the set. Roster notation is a list of elements, separated by commas, enclosed in curly braces. You can list all even numbers between 10 and 20 inside curly braces separated by a comma. The actual problem comes to the roster method with repeated elements in the set. If the elements are few, we can easily express the set in roster form as follows.
The set is represented by listing all the elements comprising it. The elements are enclosed within braces and separated by commas. These two properties are sufficient to describe each element of the set. A set is a collection of elements or numbers or objects, represented within the curly brackets .

















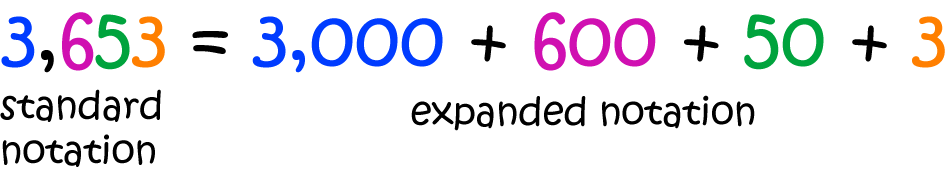


No comments:
Post a Comment
Note: Only a member of this blog may post a comment.